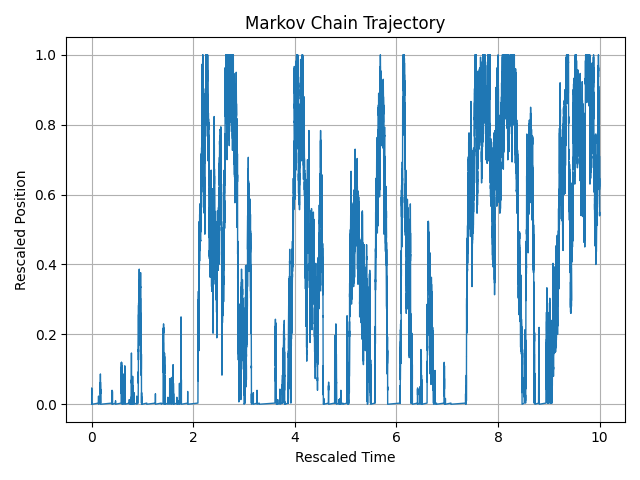
Sticky boundary at 0 ($a > -1$)
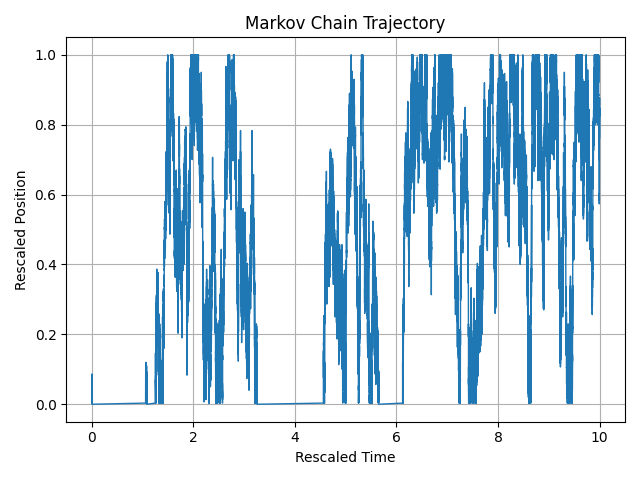
Reflecting boundaries ($a < -1$)

Intermediate regime ($a = -1$)
Page’s link: Back to GitHub README
This repository implements a discrete Markov chain approximation of a Brownian motion in $[0,1]$, with different boundary conditions at $0$, de UndeSticky Brownian Motion. The discrete dynamics depends on a parameter $a$ and, under a diffusive rescaling, for some choice of the parameter, the limiting Brownian motion is a Sticky Brownian at $0$. Other boundary behaviours at $0$, depending on $a$, show up.
We consider the discrete state space \(\{0, \tfrac{1}{N}, \tfrac{2}{N}, \dots, 1\},\) where the chain moves between adjacent points.
For implementation purposes, the states are indexed as integers: \(\{0, 1, 2, \dots, N\},\) with state $k$ corresponding to $k/N$.
Interior states ($k = 1, \dots, N-1$, corresponding to $1/N, \dots, 1-1/N$):
The jump rates are symmetric with value 1 for moving left or right.
Since the chain is a birth-death process, we can compute its invariant distribution $\pi$ using detailed balance.
For interior states: \(\pi(k+1)/\pi(k) = 1/1 = 1 \quad \implies \quad \pi(k) \; \text{constant for } k=1,\dots,N.\)
At the left boundary: \(\frac{\pi(1)}{\pi(0)} = \frac{N^{a-1}}{N^a} = \frac{1}{N}.\)
At the right boundary: \(\pi(N)/\pi(N-1) = 1.\)
Thus: \(\pi(0) \propto N, \qquad \pi(k) \propto 1 \quad (k=1,\dots,N).\)
Normalizing: \(Z = N + N = 2N,\) so \(\pi(0) = \tfrac{1}{2}, \qquad \pi(k) = \tfrac{1}{2N}, \quad k=1,\dots,N.\)
The aim is to analyze the diffusive scaling limit of the process as $N \to \infty$.
Depending on the value of the parameter $a$, we observe different limiting behaviors at the left boundary:
Case $a > -1$:
The process converges to Brownian motion with a sticky boundary condition at 0 and reflecting at 1.
Case $a < -1$:
Both boundaries become reflecting in the limit.
Case $a = -1$:
An intermediate regime where the particle spends an exponential amount of time at the origin before resuming Brownian motion.
Sticky boundary at 0 ($a > -1$)

Reflecting boundaries ($a < -1$)

Intermediate regime ($a = -1$)
